연결 리스트(Linked List)
- 연결 리스트는 길이가 정해져 있지 않은 데이터의 연결된 집합 이다
- 연결 리스트는 일렬로 연결된 데이터를 저장할 때 사용하는 자료구조이다
- 연결 리스트의 각각의 데이터는
노드라고 부르고 각 노드는data 필드와 다음 data를 바라보는주소값(next) 필드로 이뤄져있다 - 연결 리스트는
단 방향/양 방향연결리스트가 있다.
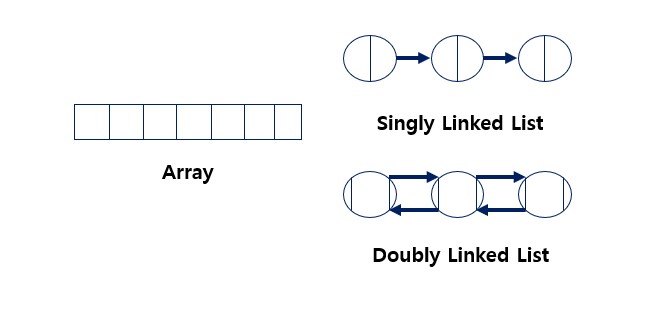
배열(Array)과 연결 리스트(Linked List)
배열과 연결 리스트는 아주 유사한 형태를 가지고 있지만 차이가 있다. 그것은 배열 의 경우 한번 선언하면 늘이거나 줄일 수 없다 는 것 이다.
단 방향 연결 리스트 Code(C++)
#include <iostream>
using namespace std;
class Node {
public:
int data;
Node* next = NULL;
};
class Link {
public:
Node* head = new Node();
void addData(int d); // 데이터 추가
void deleteData(int d); // 데이터 삭제
const void printList(); // 리스트 출력
private:
int size = 0;
};
void Link::addData(int d) {
if(size == 0) {
head->data = d;
head->next = NULL;
} else {
Node *newNode = new Node();
newNode->data = d;
newNode->next = NULL;
Node *tempNode = head;
while(tempNode->next != NULL) {
tempNode = tempNode->next;
}
tempNode->next = newNode;
}
++size;
}
void Link::deleteData(int d) {
Node* tempNode = head;
while(tempNode->next != NULL) {
if(tempNode->next->data == d) {
tempNode->next = tempNode->next->next;
} else {
tempNode = tempNode->next;
}
}
}
const void Link::printList() {
Node *tempNode = head;
int tempSize = size;
while(tempNode->next != NULL) {
cout << tempNode->data << "->";
tempNode = tempNode->next;
}
cout << tempNode->data << endl;
}
int main(void) {
Link l;
l.addData(1);
l.addData(2);
l.addData(3);
l.addData(4);
l.printList();
l.deleteData(3);
l.deleteData(2);
l.printList();
return 0;
}
이 코드는 첫 번째 노드인 head 부터가 아닌 다음 노드 부터 탐색을 한다
만약 head 노드 삭제할경우 다른 노드들이 삭제된 노드를 가지게 되고 문제가 발생할 가능성이 있는 코드이다
그렇기 때문에 이 코드에서는 첫 번째 노드는 삭제를 하지 않는 것 으로 한다
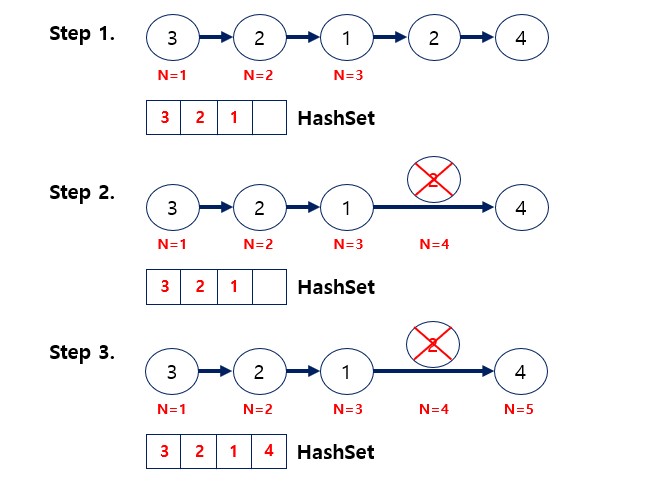
정렬되지 않은 연결 리스트 중복 값 없애기
버퍼(HashSet) 사용 예시
HashSet을 사용한 이유는 HashSet 이라는 데이터 구조는 키 값을 가지고 찾는데 O(1) 밖에 안걸리기 때문이다
- Space: O(n)
- Time: O(n)
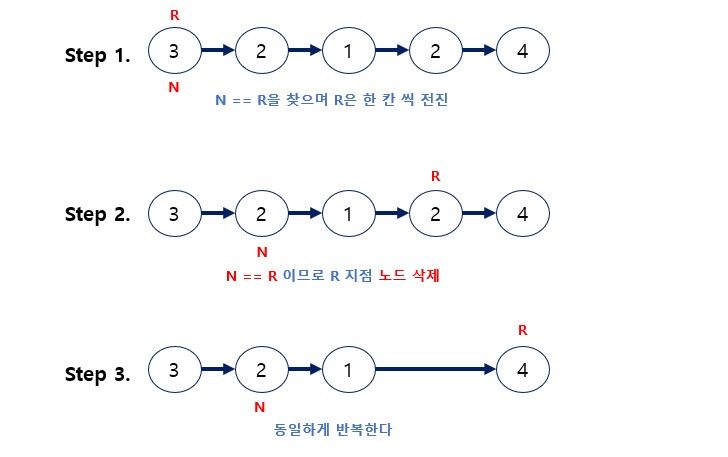
포인터(Pointer) 사용 예시
N = 0 일때 R이 List Size - n 만큼 반복하기 때문에 시간은 O(n^2)이 소요된다
또한, 고정된 Pointer 2개만 사용했기 때문에 공간은 O(1) 이다
따라서, Buffer이용한 알고리즘에 비해 시간은 더 많이 소모되지만 공간의 효율이 좋은 알고리즘이다
- Space: O(1)
- Time: O(n^2)
구현 Code(C++)
// ...내용 생략
class Link {
public:
Node* head = new Node();
void append(int d);
void deleteData(int d);
const void retrieved();
const void removeDups(); // 내용 추가
private:
int size = 0;
};
// ...중간 내용 생략
const void Link::removeDups() {
Node *n = head;
while(n != NULL && n->next != NULL) {
Node *r = n;
while(r->next != NULL) {
if(n->data == r->next->data) {
r->next = r->next->next;
} else {
r = r->next;
}
}
n = n->next;
}
}
int main(void) {
Link l;
l.append(3);
l.append(2);
l.append(1);
l.append(2);
l.append(4);
l.retrieved();
l.removeDups();
l.retrieved();
return 0;
}
References
- From by doorisopen
- 엔지니어대한민국
Leave a comment